Full Source on Github
A complete implementation of the Stoffle programming language is available at GitHub. This reference implementation has a lot of comments to help make reading the code easier. Feel free to open an issue if you find bugs or have questions.
In this blog post, we're going to implement the parser for Stoffle, a toy programing language built entirely in Ruby. You can read more about this project in the first part of this series.
Building a parser from scratch gave me some unexpected insights and knowledge. I guess this experience may vary from individual to individual, but I think it is safe to assume that after this article, you will have acquired or deepened your knowledge of at least one of the following:
- You will start seeing source code differently and noticing its undeniable tree-like structure much more easily;
- You will have a deeper understanding of syntactic sugar and will start seeing it everywhere, be it in Stoffle, Ruby, or even other programming languages.
I feel that a parser is a perfect example of the Pareto principle. The amount of work needed to create some extra-nice features, such as awesome error messages, is clearly greater and disproportionate to the effort required to get the basics up and running. We will focus on the essentials and leave improvements as a challenge to you, my dear reader. We may or may not handle some of the more interesting extras in a later article in this series.
Syntactic Sugar
Syntactic sugar is an expression used to denote constructs that make a language easier to use, but whose removal would not cause the programming language to lose functionality. A nice example is Ruby's
elsifconstruct. In Stoffle, we do not have such a structure, so to express the same we are forced to be more verbose:if some_condition # ... else # oops, no elsif available if another_condition # ... end end
What is a Parser?
We start with the source code, a raw sequence of characters. Then, as shown in the previous article in this series, the lexer groups these characters into sensible data structures called tokens. However, we are still left with data that are totally flat, something that still does not appropriately represent the nested nature of source code. Thus, the parser has the job of creating a tree from this sequence of characters. When it finishes its task, we will end up with data that are finally able to express how each part of our program nests and relates to each other.
The tree created by the parser is, generally, called an abstract syntax tree (AST). As the name implies, we are dealing with a tree data structure, with its root representing the program itself and the children of this program node being the many expressions that make up our program. The word abstract in AST refers to our ability to abstract away parts that, in previous steps, were explicitly present. A good example is expression terminators (new lines in the case of Stoffle); they are considered when building the AST, but we don't need a specific node type to represent a terminator. However, remember, we did have an explicit token to represent a terminator.
Wouldn't it be useful to have a visualization of an example AST? Your wish is an order! Below is a simple Stoffle program, which we will parse step-by-step later in this post, and its corresponding abstract syntax tree:
fn double: num
num * 2
end
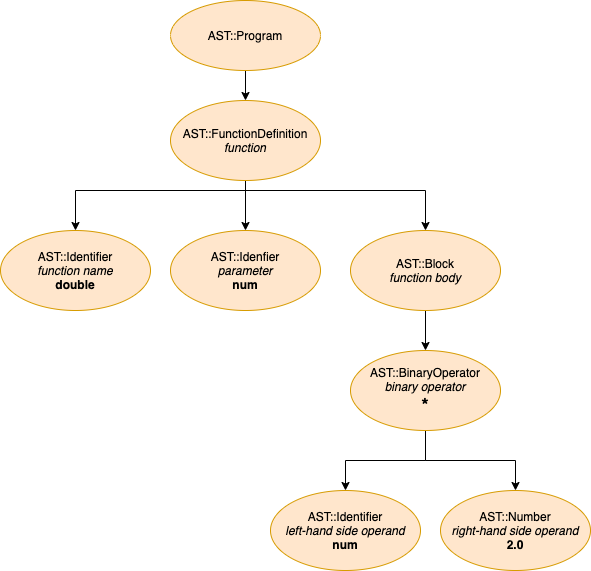
From Source to AST, a First Example
In this section of the post, we are going to explore, step-by-step, how our parser handles a very simple Stoffle program, composed of a single line in which a variable binding is expressed (i.e., we assign a value to a variable). Here's the source, a simplified representation of the tokens produced by the lexer (these tokens are the input fed to our parser) and, finally, a visual representation of the AST we are going to produce to represent the program:
Source
my_var = 1
Tokens (the Output of the Lexer, the Input for the Parser)
[:identifier, :'=', :number]
Visual Representation of the Parser's Output (an Abstract Syntax Tree)
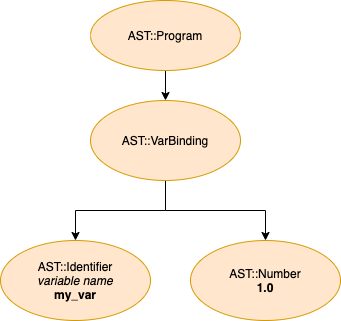
As you might imagine, the core of our parser is very similar to the core of our lexer. In the case of the lexer, we had a bunch of characters to process. Now, we still have to iterate over a collection, but in the case of the parser, we will go over the list of tokens produced by our lexer friend. We have a single pointer (@next_p) to keep track of our position in the collection of tokens. This pointer marks the next token to be processed. Although we only have this single pointer, we have many other "virtual" pointers we can use as needed; they will appear as we move along the implementation. One such "virtual" pointer is current (basically, the token at @next_p - 1).
#parse is the method to call to have the tokens transformed into an AST, which will be available at the @ast instance variable. The implementation of #parse is straightforward. We continue advancing through the collection by calling #consume and moving @next_p until there are no more tokens to be processed (i.e., while next_p < tokens.length). #parse_expr_recursively may return an AST node or nothing at all; remember, we don't need to represent terminators in the AST, for example. If a node was built in the current iteration of the loop, we add it to @ast before continuing. It's important to keep in mind that #parse_expr_recursively is also moving @next_p since, when we find a token that marks the beginning of a specific construct, we have to advance multiple times until we are able to finally build a node fully representing what we are currently parsing. Imagine how many tokens we would have to consume to build a node representing an if.
module Stoffle
class Parser
attr_accessor :tokens, :ast, :errors
# ...
def initialize(tokens)
@tokens = tokens
@ast = AST::Program.new
@next_p = 0
@errors = []
end
def parse
while pending_tokens?
consume
node = parse_expr_recursively
ast << node if node != nil
end
end
# ...
end
end
In the snippet above, for the first time, we were presented with one of the many types of AST nodes that are part of our parser implementation. Below, we have the full source code for the AST::Program node type. As you might be guessing, this is the root of our tree, representing the whole program. Let's take a closer look at the most interesting bits of it:
- A Stoffle program is composed of
@expressions; these are the#childrenof anAST::Programnode; - As you will see again, every node type implements the
#==method. As a consequence, it is easy to compare two simple nodes, as well as whole programs altogether! When comparing two programs (or two complex nodes), their equality will be determined by the equality of every children, the equality of every children of every children, and so on. This simple yet powerful strategy used by#==is extremely useful for testing our implementation.
class Stoffle::AST::Program
attr_accessor :expressions
def initialize
@expressions = []
end
def <<(expr)
expressions << expr
end
def ==(other)
expressions == other&.expressions
end
def children
expressions
end
end
Expressions vs. Statements
In some languages, many constructs don't produce a value; a conditional is a classic example. These are called statements. Other constructs, however, do evaluate to a value (e.g., a function call). These are called expressions. In other languages, however, everything is an expression and produces a value. Ruby is an example of this approach. Try, for example, typing the following snippet into IRB to find out to what value a method definition evaluates:
irb(main):001:0> def two; 2; endIf you are not feeling like firing up IRB, let me break the news to you; in Ruby, a method definition expression evaluates to a symbol (the method name). As you know, Stoffle is heavily inspired in Ruby, so in our little toy language, everything is also an expression.
Keep in mind that these definitions are good enough for practical purposes, but there is not really a consensus, and you may see the terms statement and expression being defined differently elsewhere.
Diving Deeper: Beginning the Implementation of #parse_expr_recursively
As we just saw in the snippet above, #parse_expr_recursively is the method called to potentially build a new AST node. #parse_expr_recursively does use a plethora of other smaller methods in the parsing process, but we can say with tranquility that it's the real engine of our parser. Although it's not very long, this method is more difficult to digest. Therefore, we are going to chop it into two parts. In this section of the post, let's begin with its initial segment, which is already powerful enough to parse some simpler parts of the Stoffle programming language. As a refresher, remember that we are going through the steps necessary to parse a simple program consisting of a single variable binding expression:
Source
my_var = 1
Tokens (the Output of the Lexer, the Input for the Parser)
[:identifier, :'=', :number]
After looking at the tokens we have to deal with and imagining what the lexer output would be for other, similar simple expressions, it seems like a good idea to try to associate token types with specific parsing methods:
def parse_expr_recursively
parsing_function = determine_parsing_function
if parsing_function.nil?
unrecognized_token_error
return
end
send(parsing_function)
end
In this initial implementation of #parse_expr_recursively, that's exactly what we do. Since there will be quite a lot of different token types we will have to handle, it's better to extract this decision-making process to a separate method -#determine_parsing_function, which we will see in a moment.
When we are finished, there shouldn't be any tokens we don't recognize, but as a safeguard, we will check whether a parsing function is associated with the current token. If it's not, we will add an error to our instance variable @errors, which holds all issues that happened during the parsing. We will not cover it in detail here, but you can check the full implementation of the parser at GitHub if you are curious.
#determine_parsing_function returns a symbol representing the name of the parsing method to be called. We will use Ruby's send to call the appropriate method on the fly.
Determining the Parsing Method and Parsing a Variable Binding
Next, let's take a look at #determine_parsing_function to understand this initial mechanism for calling specific methods to parse different constructs of Stoffle. #determine_parsing_function will be used for everything (e.g., keywords and unary operators) except binary operators. We will later explore the technique used in the case of binary operators. For now, let's check out #determine_parsing_function:
def determine_parsing_function
if [:return, :identifier, :number, :string, :true, :false, :nil, :fn,
:if, :while].include?(current.type)
"parse_#{current.type}".to_sym
elsif current.type == :'('
:parse_grouped_expr
elsif [:"\n", :eof].include?(current.type)
:parse_terminator
elsif UNARY_OPERATORS.include?(current.type)
:parse_unary_operator
end
end
As explained before, #current is a virtual pointer to the token being processed at the moment. The implementation of #determine_parsing_function is very straightforward; we look at the current token (specifically, its type) and return a symbol representing the appropriate method to be called.
Remember that we are going through the steps necessary to parse a variable binding (my_var = 1), so the token types we are handling are [:identifier, :'=', :number]. The current token type is :identifier, so #determine_parsing_function will return :parse_identifier, as you might be guessing. Let's glance at our next step, the #parse_identifier method:
def parse_identifier
lookahead.type == :'=' ? parse_var_binding : AST::Identifier.new(current.lexeme)
end
Here, we have a very simple manifestation of, basically, what all other parse methods do. In #parse_identifier - and in other parse methods - we check the tokens to determine whether the structure we are expecting is actually present. We know we have an identifier, but we have to look at the next token to determine whether we are dealing with a variable binding, which will be the case if the next token type is :'=', or if we just have an identifier by itself or participating in a more complex expression. Imagine, for example, an arithmetic expression in which we are manipulating values stored in variables.
Since we do have a :'=' coming next, #parse_var_binding is going to be called:
def parse_var_binding
identifier = AST::Identifier.new(current.lexeme)
consume(2)
AST::VarBinding.new(identifier, parse_expr_recursively)
end
Here, we start by creating a new AST node to represent the identifier we are currently processing. The constructor for AST::Identifier expects the lexeme of the identifier token (i.e., the sequence of characters, the string "my_var" in our case), so that is what we supply to it. We then advance two spots in the stream of tokens under processing, making the token with type :number the next one to be analyzed. Recall that we are dealing with [:identifier, :'=', :number].
Finally, we build and return an AST node representing the variable binding. The constructor for AST::VarBinding expects two parameters: an identifier AST node (the left-hand side of the binding expression) and any valid expression (the right-hand side). There is one crucial thing to note here; to produce the right-hand side of the variable binding expression, we call #parse_expr_recursively again. This might feel a little bit odd at first, but keep in mind that a variable can be bound to a very complex expression, not only to a mere number, as is the case in our example. If we were to define our parsing strategy in one word, it would be recursive. Now, I guess you are starting to grasp why #parse_expr_recursively has the name it has.
Before we finish this section, we should quickly explore both AST::Identifier and AST::VarBinding. First, AST::Identifier:
class Stoffle::AST::Identifier < Stoffle::AST::Expression
attr_accessor :name
def initialize(name)
@name = name
end
def ==(other)
name == other&.name
end
def children
[]
end
end
There's nothing fancy here. It is worth mentioning that the node stores the name of the variable and doesn't have children.
Now, AST::VarBinding:
class Stoffle::AST::VarBinding < Stoffle::AST::Expression
attr_accessor :left, :right
def initialize(left, right)
@left = left
@right = right
end
def ==(other)
children == other&.children
end
def children
[left, right]
end
end
The left-hand side is an AST::Identifier node. The right-hand side is almost every possible type of node - from a simple number, as in our example, to something more complex - representing the expression to which the identifier is bound. The #children of a variable binding are the AST nodes it holds in @left and @right.
From Source to AST, a Second Example
The current incarnation of #parse_expr_recursively is already able to parse some simple expressions, as we saw in the previous section. In this section, we will finish its implementation so that it's also able to parse more complex entities, such as binary and logical operators. Here, we will explore, step-by-step, how our parser handles a program that defines a function. Here's the source, a simplified representation of the tokens produced by the lexer and, as we had in the first section, a visual representation of the AST we will produce to represent the program:
Source
fn double: num
num * 2
end
Tokens (the Output of the Lexer, the Input for the Parser)
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
Visual Representation of the Parser Output (an Abstract Syntax Tree)

Before we move along, let's take a step back and talk about operator precedence rules. These are based on mathematical conventions; in mathematics, they are just conventions, and indeed, there's nothing fundamental that results in the operator precedence we are used to. These rules also allow us to determine the correct order for evaluating an expression and, in our case, for first parsing it. To define the precedence of each operator, we simply have a map (i.e., a Hash) of token types and integers. Higher numbers mean an operator should be handled first:
# We define these precedence rules at the top of Stoffle::Parser.
module Stoffle
class Parser
# ...
UNARY_OPERATORS = [:'!', :'-'].freeze
BINARY_OPERATORS = [:'+', :'-', :'*', :'/', :'==', :'!=', :'>', :'<', :'>=', :'<='].freeze
LOGICAL_OPERATORS = [:or, :and].freeze
LOWEST_PRECEDENCE = 0
PREFIX_PRECEDENCE = 7
OPERATOR_PRECEDENCE = {
or: 1,
and: 2,
'==': 3,
'!=': 3,
'>': 4,
'<': 4,
'>=': 4,
'<=': 4,
'+': 5,
'-': 5,
'*': 6,
'/': 6,
'(': 8
}.freeze
# ...
end
end
The technique used in #parse_expr_recursively is based on the famous parser algorithm presented by computer scientist Vaughan Pratt in his 1973 paper, "Top Down Operator Precedence". As you will see, the algorithm is very simple, but a bit difficult to fully grasp. One could say that it feels a little bit magical. What we will do in this post to try to gain an intuitive understanding of the workings of this technique is go, step-by-step, through what happens as we parse the Stoffle snippet mentioned above. So, without further ado, here is the completed version of #parse_expr_recursively:
def parse_expr_recursively(precedence = LOWEST_PRECEDENCE)
parsing_function = determine_parsing_function
if parsing_function.nil?
unrecognized_token_error
return
end
expr = send(parsing_function)
return if expr.nil? # When expr is nil, it means we have reached a \n or a eof.
# Note that, here, we are checking the NEXT token.
while nxt_not_terminator? && precedence < nxt_precedence
infix_parsing_function = determine_infix_function(nxt)
return expr if infix_parsing_function.nil?
consume
expr = send(infix_parsing_function, expr)
end
expr
end
#parse_expr_recursively now accepts a parameter, precedence. It represents the precedence "level" to be considered in a given call of the method. Additionally, the first part of the method is pretty much the same. Then - if we were able to build an expression in this first part - comes the novel piece of the method. While the next token is not a terminator (i.e., a line break or the end of the file) and the precedence (the precedence param) is lower than the precedence of the next token, we potentially continue consuming the token stream.
Before looking inside the while, let's think a little bit about the meaning of its second condition (precedence < nxt_precedence). If the precedence of the next token is higher, the expression we have just built (the expr local variable) is probably a child of a node yet to be built (remember that we are building an AST, an abstract syntax tree). Before going through the parsing of our Stoffle snippet, let's reflect on the parsing of a simple arithmetic expression: 2 + 2. When parsing this expression, the first part of our method would build an AST::Number node representing the first 2 and store it in expr. Then, we would step into the while because the precedence of the next token (:'+') would be higher than the default precedence. We would then have the parsing method to handle a sum called, passing it the AST::Number node and receiving back a node representing a binary operator (AST::BinaryOperator). Finally, we would overwrite the value stored in expr, the node representing the first 2 in 2 + 2, with this new node representing the plus operator. Notice that in the end, this algorithm allowed us to rearrange the nodes; we began with building the AST::Number node and ended up with it being a deeper node in our tree, as one of the children of the AST::BinaryOperator node.
Parsing a Function Definition Step-by-Step
Now that we have gone through an overall explanation of #parse_expr_recursively, let's return to our simple function definition:
fn double: num
num * 2
end
Even the idea of taking a look at a simplified description of the parser execution as we parse this snippet may feel tiresome (and, indeed, maybe it is!), but I think it's very valuable for better understanding both #parse_expr_recursively and the parsing of specific bits (the function definition and the product operator). First things first, here are the token types we will be dealing with (below is the output for @tokens.map(&:type), inside the parser after the lexer finished tokenizing the snippet we just saw):
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
The table below shows the order in which the most important methods are called as we parse the tokens above. Keep in mind that this is a simplification, and if you want to really understand all the exact steps of the parser execution, I recommend using a Ruby debugger, such as Byebug, and advance line-by-line as the program executes.
Our Parser Under a Microscope
There is a test that uses this exact snippet we are exploring, which is available in the source of Stoffle. You can find it inside spec/lib/stoffle/parser_spec.rb; it's the test that uses the snippet called
complex_program_ok_2.sfe.To explore parser execution step-by-step, you can edit the source and add a call to
byebugat the beginning ofParser#parse, run only the aforementioned test with RSpec, and then use Byebug'sstepcommand to advance the program one line at a time.See more information about how Byebug works and all the available commands by visiting the project's README file at GitHub.
| Method called | Current token | Next token | Notable variables / call results | Obs |
|---|---|---|---|---|
| parse | nil | :fn | ||
| parse_expr_recursively | :fn | :identifier | precedence = 0, parsing_function = :parse_fn | |
| parse_function_definition | :fn | :identifier | parse_fn is an alias of parse_function_definition | |
| parse_function_params | :identifier | :":" | ||
| parse_block | :"\n" | :identifier | ||
| parse_expr_recursively | :identifier | :* | precedence = 0, parsing_function = :parse_identifier, nxt_precedence() returns 6, infix_parsing_function = :parse_binary_operator | |
| parse_identifier | :identifier | :* | ||
| parse_binary_operator | :* | :number | op_precedence = 6 | |
| parse_expr_recursively | :number | :"\n" | precedence = 6, parsing_function = :parse_number, nxt_precedence() returns 0 | |
| parse_number | :number | :"\n" |
Now that we have a general notion of which methods are called, as well as the sequence, let's study some of the parsing methods we have not yet seen in greater detail.
The #parse_function_definition Method
The method #parse_function_definition was called when the current token was :fn and the next one was :identifier:
def parse_function_definition
return unless consume_if_nxt_is(build_token(:identifier))
fn = AST::FunctionDefinition.new(AST::Identifier.new(current.lexeme))
if nxt.type != :"\n" && nxt.type != :':'
unexpected_token_error
return
end
fn.params = parse_function_params if nxt.type == :':'
return unless consume_if_nxt_is(build_token(:"\n", "\n"))
fn.body = parse_block
fn
end
#consume_if_nxt_is - as you might be guessing - advances our pointer if the next token is of a given type. Otherwise, it adds an error to @errors. #consume_if_nxt_is is very useful - and is used in many parser methods - when we want to check the structure of the tokens to determine whether we have valid syntax. After doing that, the current token is of type :identifier (we are handling 'double', the name of the function), and we build an AST::Identifier and pass it to the constructor for creating a node to represent a function definition (AST::FunctionDefinition). We are not going to see it in detail here, but basically, an AST::FunctionDefinition node expects the function name, potentially an array of parameters and the function body.
The next step in #parse_function_definition is to verify whether the next token after the identifier is an expression terminator (i.e., a function without params) or a colon (i.e., a function with one or multiple parameters). If we do have parameters, as is the case with the double function we are defining, we call #parse_function_params to parse them. We will check out this method in a moment, but let's first continue and finish our exploration of #parse_function_definition.
The last step is to do another syntax check to verify that there is a terminator after the function name + params and, then, proceed to parse the function body by calling #parse_block. Finally, we return fn, which holds our fully-built AST::FunctionDefinition instance, complete with a function name, parameters, and a body.
The Nuts and Bolts of Function Parameters Parsing
In the previous section, we saw that #parse_function_params gets called inside #parse_function_definition. If we go back to our table summarizing the execution flow and state of our parser, we can see that when #parse_function_params starts running, the current token is of type :identifier, and the next one is :":" (i.e., we have just finished parsing the function name). With all of this in mind, let's look at some more code:
def parse_function_params
consume
return unless consume_if_nxt_is(build_token(:identifier))
identifiers = []
identifiers << AST::Identifier.new(current.lexeme)
while nxt.type == :','
consume
return unless consume_if_nxt_is(build_token(:identifier))
identifiers << AST::Identifier.new(current.lexeme)
end
identifiers
end
Before I explain each part of this method, let's recap the tokens we have to process and where we are in this job:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# here ▲
The first part of #parse_function_params is straightforward. If we have valid syntax (at least one identifier after the :), we end up moving our pointer by two positions:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# ▲
Now, we are sitting at the first parameter to be parsed (a token of type :identifier). As expected, we create an AST::Identifier and push it to an array of, potentially, multiple other parameters yet to be parsed. In the next bit of #parse_function_params, we continue parsing params as long as there are parameter separators (i.e., tokens of type :','). We end the method by returning the local var identifiers, an array with, potentially, multiple AST::Identifier nodes, each representing one param. However, in our case, this array has only one element.
What About the Function Body?
Now let's dive deep into the last part of parsing a function definition: dealing with its body. When #parse_block is called, we are sitting at the terminator that marked the end of the list of function parameters:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# ▲
And, here's the implementation of #parse_block:
def parse_block
consume
block = AST::Block.new
while current.type != :end && current.type != :eof && nxt.type != :else
expr = parse_expr_recursively
block << expr unless expr.nil?
consume
end
unexpected_token_error(build_token(:eof)) if current.type == :eof
block
end
AST::Block is the AST node for representing, well, a block of code. In other words, AST::Block just holds a list of expressions, in a very similar fashion as the root node of our program, an AST::Program node (as we saw at the beginning of this post). To parse the block (i.e., the function body), we continue advancing through unprocessed tokens until we encounter a token that marks the end of the block.
To parse the expressions that compose the block, we use our already-known #parse_expr_recursively. We will step into this method call in just a moment; this is the point in which we will start parsing the product operation happening inside our double function. Following this closely will allow us to understand the use of precedence values inside #parse_expr_recursively and how an infix operator (the * in our case) gets dealt with. Before we do that, however, let's finish our exploration of #parse_block.
Before returning an AST node representing our block, we check whether the current token is of type :eof. If this is the case, we have a syntax error since Stoffle requires a block to end with the end keyword. To wrap up the explanation of #parse_block, I should mention something you have probably noticed; one of the conditions of our loop verifies whether the next token is of type :else. This happens because #parse_block is shared by other parsing methods, including the methods responsible for parsing conditionals and loops. Pretty neat, huh?!
Parsing Infix Operators
The name may sound a bit fancy, but infix operators are, basically, those we are very used to seeing in arithmetic, plus some others that we may be more familiar with by being software developers:
module Stoffle
class Parser
# ...
BINARY_OPERATORS = [:'+', :'-', :'*', :'/', :'==', :'!=', :'>', :'<', :'>=', :'<='].freeze
LOGICAL_OPERATORS = [:or, :and].freeze
# ...
end
end
They are expected to be used infixed when the infix notation is used, as is the case with Stoffle, which means they should appear in the middle of their two operands (e.g., as * appears in num * 2 in our double function). Something worth mentioning is that although the infix notation is pretty popular, there are other ways of positioning operators in relation to their operands. If you are curious, research a little bit about "Polish notation" and "reverse Polish notation" methods.
To finish parsing our double function, we have to deal with the * operator:
fn double: num
num * 2
end
In the previous section, we mentioned that parsing the expression that composes the body of double starts when #parse_expr_recursively is called within #parse_block. When that happens, here's our position in @tokens:
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
# ▲
And, to refresh our memory, here's the code for #parse_expr_recursively again:
def parse_expr_recursively(precedence = LOWEST_PRECEDENCE)
parsing_function = determine_parsing_function
if parsing_function.nil?
unrecognized_token_error
return
end
expr = send(parsing_function)
return if expr.nil? # When expr is nil, it means we have reached a \n or a eof.
# Note that here, we are checking the NEXT token.
while nxt_not_terminator? && precedence < nxt_precedence
infix_parsing_function = determine_infix_function(nxt)
return expr if infix_parsing_function.nil?
consume
expr = send(infix_parsing_function, expr)
end
expr
end
In the first part of the method, we will use the same #parse_identifier method we used to parse the num variable. Then, for the first time, the conditions of the while loop will evaluate to true; the next token is not a terminator, and the precedence of the next token is greater than the precedence of this current execution of parse_expr_recursively (precedence is the default, 0, while nxt_precedence returns 6 since the next token is of type :'*'). This indicates that the node we already built (an AST::Identifier representing num) will probably be deeper in our AST (i.e., it will be the child of a node yet to be built). We enter the loop and call #determine_infix_function, passing to it the next token (the *):
def determine_infix_function(token = current)
if (BINARY_OPERATORS + LOGICAL_OPERATORS).include?(token.type)
:parse_binary_operator
elsif token.type == :'('
:parse_function_call
end
end
Since * is a binary operator, running #determine_infix_function will result in :parse_binary_operator. Back in #parse_expr_recursively, we will advance our tokens pointer by one position and then call #parse_binary_operator, passing along the value of expr (the AST::Identifier representing num):
[:fn, :identifier, :":", :identifier, :"\n", :identifier, :*, :number, :"\n", :end, :"\n", :eof]
#▲
def parse_binary_operator(left)
op = AST::BinaryOperator.new(current.type, left)
op_precedence = current_precedence
consume
op.right = parse_expr_recursively(op_precedence)
op
end
class Stoffle::AST::BinaryOperator < Stoffle::AST::Expression
attr_accessor :operator, :left, :right
def initialize(operator, left = nil, right = nil)
@operator = operator
@left = left
@right = right
end
def ==(other)
operator == other&.operator && children == other&.children
end
def children
[left, right]
end
end
At #parse_binary_operator, we create an AST::BinaryOperator (its implementation is shown above if you are curious) to represent *, setting its left operand to the identifier (num) we received from #parse_expr_recursively. Then, we save the precedence value of * at the local var op_precedence and advance our token pointer. To finish building our node representing *, we call #parse_expr_recursively again! We need to proceed in this fashion because the right-hand side of our operator will not always be a single number or identifier; it can be a more complex expression, such as something like num * (2 + 2).
One thing of utmost importance that happens here at #parse_binary_operator is the way in which we call #parse_expr_recursively back again. We call it passing 6 as a precedence value (the precedence of *, stored at op_precedence). Here we observe an important aspect of our parsing algorithm, which was mentioned previously. By passing a relatively high precedence value, it seems like * is pulling the next token as its operand. Imagine we were parsing an expression like num * 2 + 1; in this case, the precedence value of * passed in to this next call to #parse_expr_recursively would guarantee that the 2 would end up being the right-hand side of * and not an operand of +, which has a lower precedence value of 5.
After #parse_expr_recursively returns an AST::Number node, we set it as the right-hand size of * and, finally, return our complete AST::BinaryOperator node. At this point, we have, basically, finished parsing our Stoffle program. We still have to parse some terminator tokens, but this is straightforward and not very interesting. At the end, we will have an AST::Program instance at @ast with expressions that could be visually represented as the tree we saw at the beginning of this post and in the introduction to the second section of the post:

Wrapping Up
In this post, we covered the principal aspects of Stoffle's parser. If you understand the bits we explored here, you shouldn't have much trouble understanding other parser methods we were not able to cover, such as parsing conditionals and loops. I encourage you to explore the source code of the parser by yourself and tweak the implementation if you are feeling more adventurous! The implementation is accompanied by a comprehensive test suite, so don't be afraid to try things out and mess up with the parser.
In subsequent posts in this series, we will finally breathe life into our little monster by implementing the last bit we are missing: the tree-walk interpreter. I can't wait to be there with you as we run our first Stoffle program!
 By
By 

 Molly Struve, Sr. Site Reliability Engineer, Netflix
Molly Struve, Sr. Site Reliability Engineer, Netflix
 Chris Patton, Founder of Punchpass.com
Chris Patton, Founder of Punchpass.com
