Fiddle is a little-known module that was added to Ruby's standard library in 1.9.x. It allow you to interact directly with C libraries from Ruby. It even lets you inspect and alter the ruby interpreter as it runs.
It works by wrapping libffi, a popular C library that allows code written in one language to call methods written in another. In case you haven't heard of it, "ffi" stands for "foreign function interface." And you're not just limited to C. Once you learn Fiddle, you can use libraries written in Rust and other languages that support it.
Let's take a look at Fiddle. We'll start out with a simple example and then end by accessing an Arduino over a serial port. You don't need to know that much C. I promise. :)
A simple example
In plain-old Ruby, you always have to define a method before you can call it. It's the same with Fiddle. You can't just call a C function directly. Instead you have to create a wrapper for the C function, then call the wrapper.
In the example below, we're wrapping C's logarithm function. We're basically duplicating Ruby's Math.log.
require 'fiddle'
# We're going to "open" a library, so we have to tell Fiddle where
# it's located on disk. This example works on OSX Yosemite.
libm = Fiddle.dlopen('/usr/lib/libSystem.dylib')
# Create a wrapper for the c function "log".
log = Fiddle::Function.new(
libm['log'], # Get the function from the math library we opened
[Fiddle::TYPE_DOUBLE], # It has one argument, a double, which is similar to ruby's Float
Fiddle::TYPE_DOUBLE # It returns a double
)
# call the c function via our wrapper
puts log.call(3.14159)
Making it pretty
The previous example works, but it's kind of verbose. I'm sure you can imagine how cluttered things would get if you had to wrap 100 functions. That's why Fiddle provides a nice DSL. It's exposed via the Fiddle::Importer mixin.
Using this mixin makes it short work to create a module full of external functions. In the example below, we're creating a module that contains several logarithm methods.
require 'fiddle'
require 'fiddle/import'
module Logs
extend Fiddle::Importer
dlload '/usr/lib/libSystem.dylib'
extern 'double log(double)'
extern 'double log10(double)'
extern 'double log2(double)'
end
# We can call the external functions as if they were ruby methods!
puts Logs.log(10) # 2.302585092994046
puts Logs.log10(10) # 1.0
puts Logs.log2(10) # 3.321928094887362
Controling the serial port
Ok, so you finally bought one of those Arduinos you've been thinking about buying for years. You've got sending the text "hello world" to your computer once per second using the serial port.
Now, it'd be really nice if you could read that data using Ruby. And you can actually read from the serial port using Ruby's standard IO methods. But these IO methods don't let us configure the serial input with the level of granularity that we need if we're to be hardcore hardware hackers.
Fortunately, the C standard library provides all the functions we need to work with the serial port. And using Fiddle, we can access these C functions in Ruby.
Of course, there are already gems that do this for you. When I was working on this code I took a little inspiration from the rubyserial gem. But our goal is to learn how to do this stuff ourselves.
Examining termios.h
In C, any filename ending in .h is a header file. It contains a list of all functions and constants that the library makes available to third party code (our code). The first step in wrapping any C library is going to be to find this file, open it and look around.
The library we're using is called termios. On OSX Yosemite, the header file is located at /usr/include/sys/termios.h. It will be somewhere else on linux.
Here's what termios.h looks like. I've condensed it quite a bit for clarity.
typedef unsigned long tcflag_t;
typedef unsigned char cc_t;
typedef unsigned long speed_t;
struct termios {
tcflag_t c_iflag; /* input flags */
tcflag_t c_oflag; /* output flags */
tcflag_t c_cflag; /* control flags */
tcflag_t c_lflag; /* local flags */
cc_t c_cc[NCCS]; /* control chars */
speed_t c_ispeed; /* input speed */
speed_t c_ospeed; /* output speed */
};
int tcgetattr(int, struct termios *);
int tcsetattr(int, int, const struct termios *);
int tcflush(int, int);
There are three important things to notice about this code. First, we have some typedefs. Then we have a data structure which is used to hold configuration info for the connection. Finally, we have the methods, we're going to use.
Using fiddle's importer, we can almost copy these sections verbatim into our Ruby code. Let's tackle them one by one.
Type aliases and typedefs
In C it's pretty common to create aliases for data types. For example, the termios.h file creates a new type called speed_t that is just a long integer. The Fiddle importer is able to handle these via its typealias feature.
# equivalent to `typedef unsigned long tcflag_t;`
typealias "tcflag_t", "unsigned long"
Structs
C doesn't have classes or modules. If you want to group a bunch of variables together, you use a struct. Fiddle provides a nice mechanism for working with structs in ruby.
The first step is to define the struct in the Fiddle importer. As you can see, we're almost able to just copy and paste from the header file.
Termios = struct [
'tcflag_t c_iflag',
'tcflag_t c_oflag',
'tcflag_t c_cflag',
'tcflag_t c_lflag',
'cc_t c_cc[20]',
'speed_t c_ispeed',
'speed_t c_ospeed',
]
Now we can create an "instance" of the struct by using the malloc method. We can set and retrieve values in much the same way that we would with any normal Ruby class instance.
s = Termios.malloc
s.c_iflag = 12345
Putting it all together
If you combine what we just learned about typedefs and structs with what we've already demonstrated with functions, we can put together a working wrapper of the termios library.
Our wrapper just contains the methods we need to configure the serial port. We'll use plain old ruby for the rest.
require 'fiddle'
require 'fiddle/import'
# Everything in this module was pretty much copied directly from
# termios.h. In Yosemite it's at /usr/include/sys/termios.h
module Serial
extend Fiddle::Importer
dlload '/usr/lib/libSystem.dylib'
# Type definitions
typealias "tcflag_t", "unsigned long"
typealias "speed_t", "unsigned long"
typealias "cc_t", "char"
# A structure which will hold configuratin data. Instantiate like
# so: `Serial::Termios.malloc()`
Termios = struct [
'tcflag_t c_iflag',
'tcflag_t c_oflag',
'tcflag_t c_cflag',
'tcflag_t c_lflag',
'cc_t c_cc[20]',
'speed_t c_ispeed',
'speed_t c_ospeed',
]
# Functions for working with a serial device
extern 'int tcgetattr(int, struct termios*)' # get the config for a serial device
extern 'int tcsetattr(int, int, struct termios*)' # set the config for a serial device
extern 'int tcflush(int, int)' # flush all buffers in the device
end
Using the library
In the example below we open our serial device in Ruby, then get its file descriptor. We use our termios functions to configure the device for reading. Then we read.
I'm making use of some magic numbers here. These are the result of combining a bunch of bitwise configuration options that are necessary for communication with the arduino. If you're interested in where the magic numbers come from, check out this blog post.
file = open("/dev/cu.wchusbserial1450", 'r')
fd = file.to_i
# Create a new instance of our config structure
config = Serial::Termios.malloc
# Load the default config options into our struct
Serial.tcgetattr(fd, config);
# Set config options important to the arduino.
# I'm sorry for the magic numbers.
config.c_ispeed = 9600;
config.c_ospeed = 9600;
config.c_cflag = 51968;
config.c_iflag = 0;
config.c_oflag = 0;
# wait for 12 characters to come in before read returns.
config.c_cc[17] = 12;
# no minimum time to wait before read returns
config.c_cc[16] = 0;
# Save our configuration
Serial.tcsetattr(fd, 0, config);
# Wait 1 second for the arduino to reboot
sleep(1)
# Remove any existing serial input waiting to be read
Serial.tcflush(fd, 1)
buffer = file.read(12)
puts "#{ buffer.size } bytes: #{ buffer }"
file.close
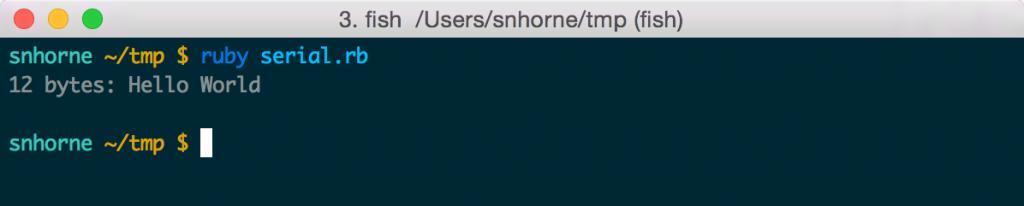
The serial reader in action
If I now load my arduino with a program that continuously prints hello world, I can use my ruby script to read it.
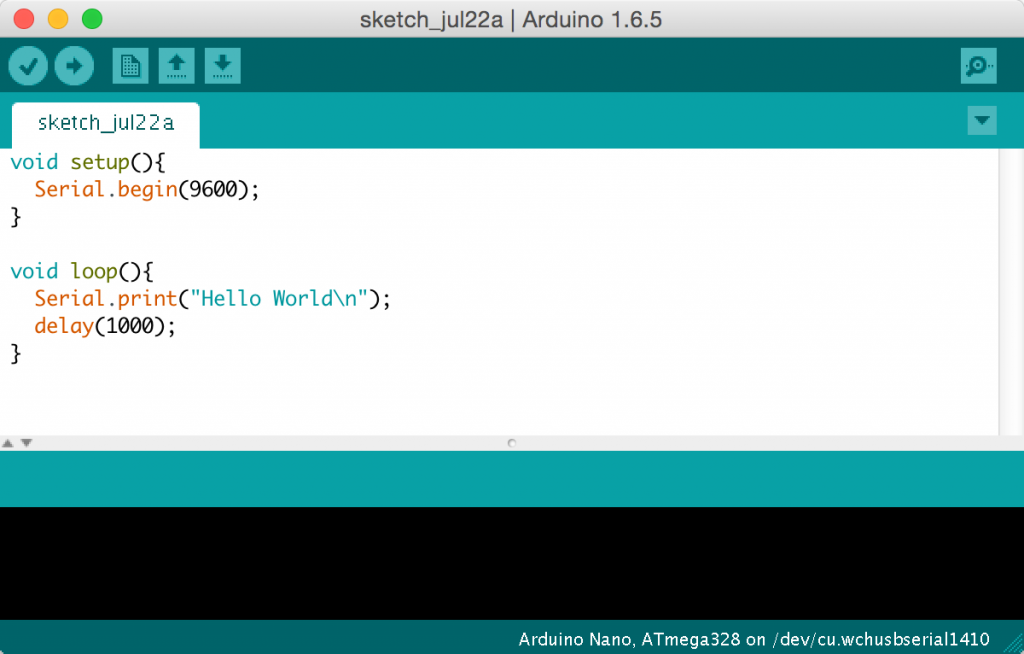 This arduino program just writes "hello world" to serial, again and again
This arduino program just writes "hello world" to serial, again and again
And here's what it looks like when I run my serial monitor.