By RBS is the name of a new type syntax format language for Ruby. RBS lets you add type annotations to your Ruby code in files with a new extension called .rbs. They look like this:
class MyClass
def my_method : (my_param: String) -> String
end
By providing type annotations with RBS you get benefits such as:
- a clean and concise way to define the structure of your codebase.
- a safer way to add types to your legacy code via files rather than changing the classes directly.
- the potential to universally integrate with static and dynamic type checkers.
- new features to deal with method overloading, duck typing, dynamic interfaces, and more.
But wait! Aren't there already static type checkers like Sorbet and Steep?
Yes, and they're great! However, after four years of discussion and a handful of community-built type checkers, the Ruby committer team thought it was time to define some standards for building type checker tools.
RBS is officially a language, and it's coming to life along with Ruby 3.
Plus, due to Ruby's dynamically typed nature, as well as common patterns like Duck Typing and method overloading, some precautions are being instituted to ensure the best approach possible, which we'll see in more detail shortly.
Ruby 3 Install
To follow the examples shown here, we need to install Ruby 3.
You can do it either by following the official instructions or via ruby-build in case you need to manage many Ruby versions.
Alternatively, you can also install the rbs gem directly into your current project:
gem install rbs
Static vs Dynamic Typing
Before going any further, let's clarify this concept. How do dynamically typed languages compare to static ones?
In dynamically typed languages, such as Ruby and JavaScript, there are no predefined data types for the interpreter to understand how to proceed in case a forbidden operation happens during runtime.
That is the opposite of what's expected from static typing. Statically typed languages, such as Java and C, verify the types during compile time.
Take the following Java code snippet as a reference:
int number = 0;
number = "Hi, number!";
This is not possible in static typing, since the second line will throw an error:
error: incompatible types: String cannot be converted to int
Now, take the same example in Ruby:
number = 0;
number = "Hi, number!";
puts number // Successfully prints "Hi, number!"
In Ruby, the type of a variable varies on the fly, which means that the interpreter knows how to dynamically swap from one to another.
That concept is commonly confused with strongly typed vs weakly typed languages.
Ruby is not only a dynamically but also strongly typed language, which means that it allows for a variable to change its type during runtime. It does not, however, allow you to perform crazy type mixing operations.
Take the next example (in Ruby) adapted from the previous one:
number = 2;
sum = "2" + 2;
puts sum
This time we're trying a sum of two numbers that belong to different types (an Integer and a String). Ruby will throw the following error:
main.rb:2:in `+': no implicit conversion of Integer into String (TypeError)
from main.rb:2:in `<main>'
In other words, Ruby's saying that the job for performing complex calculations involving (possibly) different types is all yours.
JavaScript, on the other hand, which is weakly and dynamically typed, allows the same code with a different result:
> number = 2
sum = "2" + 2
console.log(sum)
> 22 // it concatenates both values
How does RBS differ from Sorbet?
First, from the approach that each one takes to annotating code. While Sorbet works by explicitly adding annotations throughout your code, RBS simply requires the creation of a new file with the .rbs extension.
The primary advantage of this is when we think about the migration of legacy codebases. Since your original files won't get affected, it's much safer to adopt RBS files into your projects.
According to its creators, RBS’ main goal is to describe the structure of your Ruby programs. It focuses on defining class/method signatures only.
RBS itself can't type check. Its goal is restricted to defining the structure as a basis for type checkers (like Sorbet and Steep) to do their job.
Let's see an example of a simple Ruby inheritance:
class Badger
def initialize(brand)
@brand = brand
end
def brand?
@brand
end
end
class Honey < Badger
def initialize(brand: "Honeybadger", sweet: true)
super(brand)
@sweet = sweet
end
def sweet?
@sweet
end
end
Great! Just two classes with a few attributes and inferred types.
Below, we can see a possible RBS representation:
class Brand
attr_reader brand : String
def initialize : (brand: String) -> void
end
class Honey < Brand
@sweet : bool
def initialize : (brand: String, ?sweet: bool) -> void
def sweet? : () -> bool
end
Pretty similar, aren't they? The major difference here is the types. The initialize method of the Honey class, for example, receives one String and one boolean parameter and returns nothing.
Meanwhile, the Sorbet team is working closely on the creation of tools to allow interoperability between RBI (Sorbet's default extension for type definition) and RBS.
The goal is to lay the groundwork for Sorbet and any type checker to understand how to make use of RBS' type definition files.
Scaffolding Tool
If you're starting with the language and already have some projects going on, it could be hard to guess where and how to start typing things around.
With this in mind, the Ruby team provided us with a very helpful CLI tool called rbs to scaffold types for existing classes.
To list the available commands, simply type rbs help in the console and check the result:
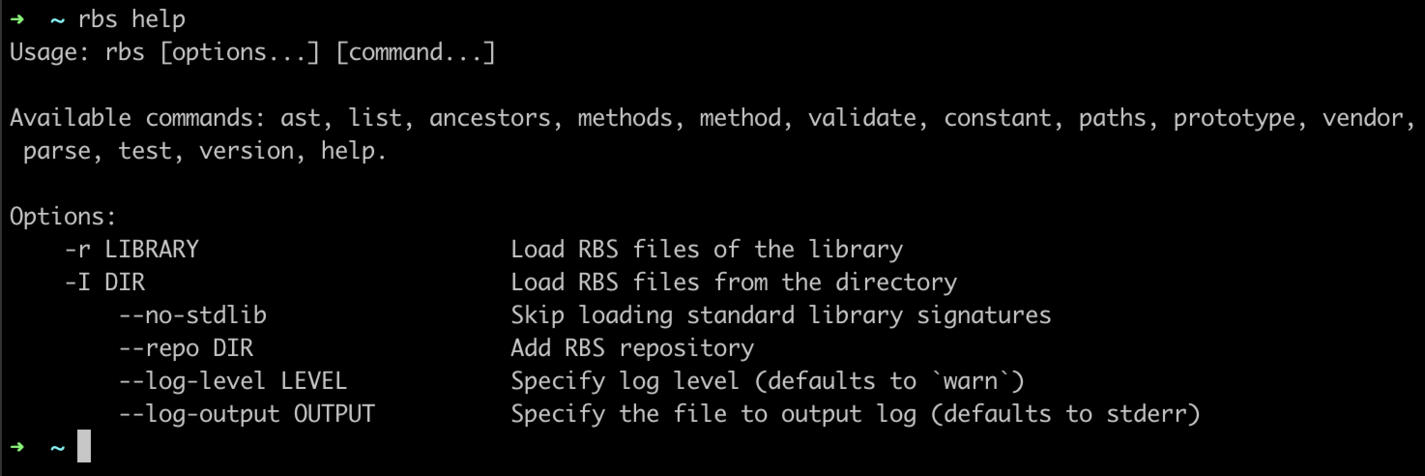Available commands in the CLI tool.
Perhaps the most important command in the list is prototype since it analyzes ASTs of the source code file provided as a param to generate "approximate" RBS code.
Approximate because it is not 100% effective. Since your legacy code is primarily untyped, most of its scaffolded content will come the same way. RBS can't guess some types if there are no explicit assignments, for example.
Let's take another example as reference, this time involving three different classes in a cascaded inheritance:
class Animal
def initialize(weight)
@weight = weight
end
def breathe
puts "Inhale/Exhale"
end
end
class Mammal < Animal
def initialize(weight, is_terrestrial)
super(weight)
@is_terrestrial = is_terrestrial
end
def nurse
puts "I'm breastfeeding"
end
end
class Cat < Mammal
def initialize(weight, n_of_lives, is_terrestrial: true)
super(weight, is_terrestrial)
@n_of_lives = n_of_lives
end
def speak
puts "Meow"
end
end
Just simple classes with attributes and methods. Note that one of them is provided with a default boolean value, which will be important to demonstrate what RBS is capable of when guessing by itself.
Now, to scaffold these types, let's run the following command:
rbs prototype rb animal.rb mammal.rb cat.rb
You can pass as many Ruby files as you wish. The following is the result of this execution:
class Animal
def initialize: (untyped weight) -> untyped
def breathe: () -> untyped
end
class Mammal < Animal
def initialize: (untyped weight, untyped is_terrestrial) -> untyped
def nurse: () -> untyped
end
class Cat < Mammal
def initialize: (untyped weight, untyped n_of_lives, ?is_terrestrial: bool is_terrestrial) -> untyped
def speak: () -> untyped
end
As we've predicted, RBS can't understand most of the types we were aiming for when we created the classes.
Most of your job will be to manually change the untyped references to the real ones. Some discussions aiming to find better ways to accomplish this are happening right now in the community .
Metaprogramming
When it comes to metaprogramming, the rbs tool won't be of much help due to its dynamic nature.
Take the following class as an example:
class Meta
define_method :greeting, -> { puts 'Hi there!' }
end
Meta.new.greeting
The following will be the result of scaffolding this type:
class Meta
end
Duck Typing
Ruby doesn't worry too much about objects’ natures (their types) but does care about what they're capable of (what they do).
Duck typing is a famous programming style that operates according to the motto:
"If an object behaves like a duck (speak, walk, fly, etc.), then it is a duck"
In other words, Ruby will always treat it like a duck even though its original definition and types were not supposed to represent a duck.
However, duck typing can hide details of the code implementation that can easily become tricky and difficult to find/read.
RBS introduced the concept of interface types, which are a set of methods that do not depend on any concrete class or module.
Let's take the previous animal inheritance example and suppose that we're adding a new hierarchical level for terrestrial animals from which our Cat will inherit to:
class Terrestrial < Animal
def initialize(weight)
super(weight)
end
def run
puts "Running..."
end
end
To avoid non-terrestrial children objects from running, we can create an interface that checks for the specific type for such an action:
interface _CanRun
# Requires `<<` operator which accepts `Terrestrial` object.
def <<: (Terrestrial) -> void
end
When mapping the RBS code to the specific run method, that'd be the signature:
def run: (_CanRun) -> void
Whenever someone tries to pass anything other than a Terrestrial object to the method, the type checker will make sure to log the error.
Union Types
It's also common among Rubyists to have expressions that hold different types of values.
def fly: () -> (Mammal | Bird | Insect)
RBS accommodates union types by simply joining them via pipe operator.
Method Overloading
Another common practice (among many programming languages actually) is to allow for method overloading, in which a class can have more than one method with the same name but the signature is different (like the types or number of params, their order, etc.).
Let's take an example in which an animal can return its closest evolutionary cousins:
def evolutionary_cousins: () -> Enumerator[Animal, void] | { (Animal) -> void } -> void
In this way, RBS allows us to explicitly determine whether a given animal will have a single evolutionary cousin or a bunch of them.
TypeProf
In parallel, the Ruby team has also started a new project called typeprof, an experimental type-level Ruby interpreter that aims to analyze and (try to) generate RBS content.
It works by abstract interpretation and is still taking the first steps towards better refinement, so be careful when using it for production purposes.
To install it, simply add the gem to your project:
gem install typeprof
Be aware that it requires a Ruby version greater than 2.7.
Take the following version of the Animal class:
class Animal
def initialize(weight)
@weight = weight
end
def die(age)
if age > 50
true
elsif age <= 50
false
elsif age < 0
nil
end
end
end
Animal.new(100).die(65)
Based on what's going on inside the method age and the further call to the same method, TypeProf can smartly infer the types manipulated in the code.
When you run the typeprof animal.rb command, that should be the output:
## Classes
class Animal
@weight: Integer
def initialize: (Integer weight) -> Integer
def die: (Integer age) -> bool?
end
It's a powerful tool that has a lot to offer for projects that already have lots of code going on.
VS Code Integration
Currently, there are not a lot of available VS Code plugins for dealing with RBS for formatting, structure checking, etc. Especially because it's still relatively new.
However, if you search in the store for "RBS" you may find one plugin called ruby-signature which will help with syntax highlighting, as shown below:
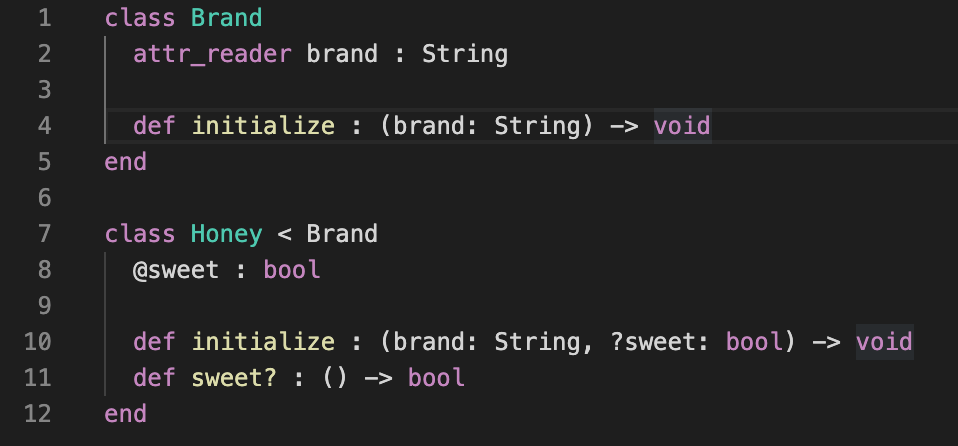RBS syntax highlighting in VS Code.
Conclusion
RBS is just so fresh and already represents an important step towards safer Ruby codebases.
Normally, in time new tools and open-source projects will rise to back it up, such as the RBS Rails for generating RBS files for Ruby on Rails applications.
The future holds amazing stuff for the Ruby community with safer and more bug-free applications. Can't wait to see it!
